Résumé L'évolution de la taille d'une population peut être retracée à partir d'un échantillon de séquences d'ADN. Dans cette thèse, nous proposons une nouvelle méthodologie non paramétrique basée sur une stratégie d'échantillonnage pondéré (Importance Sampling) qui permet d'explorer de tels historiques démographiques. L'essence de la méthode est de simuler un grand nombre de généalogies en utilisant le processus de coalescence, où l'information fournie par ces généalogies est combinée en utilisant les poids de cet échantillonnage pondéré. En premier, nous proposons la méthode skywis plot qui débute par l'estimation de la taille de la population e ective pour chaque généalogie, pour chaque intervalle de temps prédé ni, appelé époque ; ensuite, une moyenne pondérée de ces tailles de population estimées est calculée. Ainsi, les généalogies qui sont le plus en accord avec les données ont un poids plus élevé. Nous avons aussi généralisé notre méthodologie au cas d'un échantillonnage en série. Cela a nécessité la mise en ÷uvre d'une stratégie d'échantillonnage e cace qui permet de tenir compte de cette réalité qui est très utilisée, notamment dans le cas de virus qui évoluent rapidement comme le VIH. Ensuite, nous proposons d'améliorer la performance de la méthode skywis plot à travers une procédure itérative appelée iterative calibrated skywis plot ; la taille de la population e ective est approximée par une fonction en escalier, qu'on réestime après chaque itération en utilisant la méthode calibrated skywis plot. Ces fonctions en escalier sont utilisées pour générer les temps d'attente d'un processus de Poisson non homogène (coalescence avec mutation) sous un modèle avec une taille de population variable. Cela nous a aussi amené à adapter la distribution proposée de Stephens et Donnelly (2000).
Mots-clés : historique démographique, échantillonnage pondéré, processus de coalescence, skywis plot, échantillonnage hétérochrone, processus non homogène.

Introduction

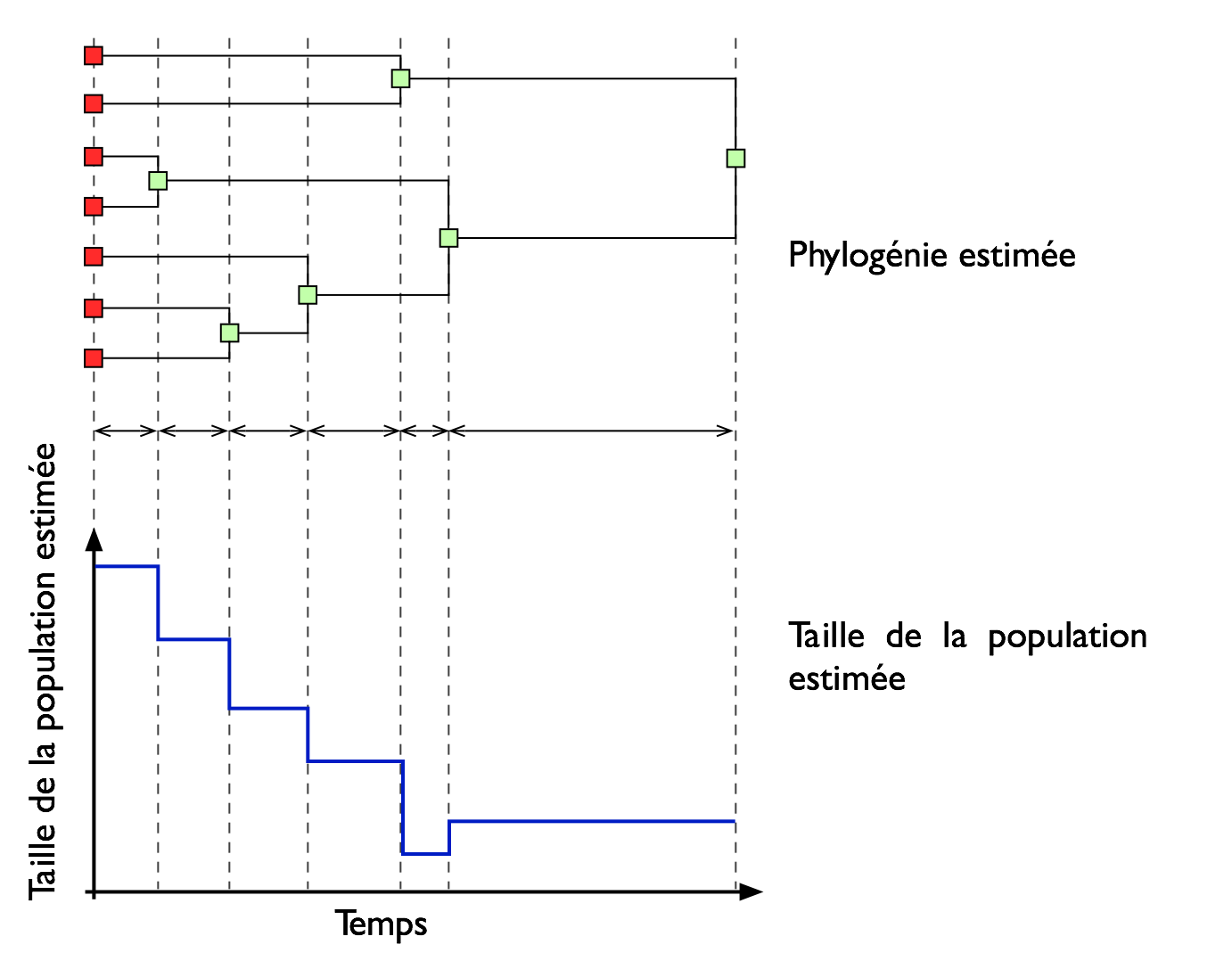
Les séquences d'ADN contiennent de l'information sur l'historique démographique de la population où les séquences ont été échantillonnées. Ainsi, avec la disponibilité de séquences complètes de plusieurs génomes de virus, le problème de l'estimation de la taille de la population est devenu un sujet important en statistique génétique, avec des applications pratiques qui permettent, par exemple, de prédire l'évolution des virus, d'étudier le lien entre les événements démographiques et climatiques, ou encore retracer la transmission et la propagation des virus. Dans cette thèse, nous proposons une nouvelle méthodologie non paramétrique exible où la connaissance de la fonction analytique qui régit la taille de la population e ective n'est pas nécessaire. Dans le premier chapitre, nous présentons les concepts de base de la biologie moléculaire, dont le but est de familiariser le lecteur avec les termes nécessaires à la compréhension des mécanismes d'évolution virale, comme la mutation qui est au c÷ur du sujet traité. Nous décrivons ensuite au chapitre 2 la théorie de coalescence, en commençant par le processus de coalescence classique qui suppose, entre autres, que la taille de la population reste constante à travers le temps. Cette hypothèse est ensuite levée en présentant le processus de coalescence dans le cas où la taille de population e ective est variable, ainsi qu'en présence de la recombinaison. Au chapitre 3, on s'intéresse aux méthodes qui permettent d'approximer la vraisemblance L(θ) en utilisant l'échantillonnage pondéré. En particulier, on décrit en détails la distribution proposée par Stephens et Donnelly (2000), qui permet de simuler des généalogies de manière e cace. Le chapitre 4, quant à lui, décrit les méthodes non paramétriques appelées skyline plot qui permettent d'estimer la taille de la population e ective. En e et, notre méthodologie peut être considérée comme une amélioration de la méthode skyline plot classique. Les chapitres 5 et 6 sont constitués de deux articles scienti ques en langue anglaise, qui présentent nos nouvelles méthodes. Le chapitre 5 décrit la méthode skywis plot qui s'appuie sur la simulation d'un grand nombre de généalogies en utilisant un échantillonnage pondéré. Ainsi, la taille de la population e ective est d'abord estimée pour chacune des généalogies sur un nombre donné d'époques ; ces époques sont obtenues par cumul de temps de coalescence. Ensuite, une moyenne pondérée des estimés de la taille de la population e ective est calculée pour chacune des époques, où les poids utilisés sont issus de l'échantillonnage pondéré. Notre méthode permet notamment d'a ecter un plus grand poids aux généalogies les plus vraisemblables avec les séquences échantillonnées. De plus, notre méthodologie est généralisée au cas d'un échantillonnage hétérochrone. À cet e et, une nouvelle fonction d'importance est proposée a n de simuler des généalogies dans un cadre où les séquences étudiées sont échantillonnées à des intervalles de temps assez importants. Ainsi, nous montrons par simulation qu'un échantillonnage hétérochrone permet d'améliorer la qualité de l'estimation de l'historique démographique quand on se rapproche de l'ancêtre commun. Notons que cet article a été publié dans la revue Frontiers in Genetics, section Evolutionary and Population Genetics. Le chapitre 6 décrit, à travers un deuxième article scienti que qui a été soumis, la méthode appelée iterative calibrated skywis plot ; cette méthode permet d'améliorer la performance du skywis plot dans le cas d'une évolution très rapide de la taille de la population e ective. Cela est réalisé en approximant au préalable la taille de la population par un modèle où la taille de population est variable, mais constante par intervalle. Dans ce cas, le taux de coalescence est di érent d'un intervalle à un autre, ce qui a nécessité d'adapter la fonction d'importance de Stephens et Donnelly (2000) à cette problématique où le processus d'arrivée des événements (coalescence ou mutation) devient non-homogène.

Conclusion

En nous basant sur la théorie de coalescence, nous avons proposé une nouvelle méthode non paramétrique, le skywis plot, qui permet d'explorer l'historique démographique d'un échantillon de séquences d'ADN. La méthode du skywis plot est basée sur la simulation d'un grand nombre de généalogies en utilisant un échantillonnage pondéré, où les poids résultants sont utilisés pour le calcul d'une moyenne pondérée des tailles de population e ective par époque ; cela permet de produire de bons estimés qui détectent bien la tendance évolutive de la taille de population e ective à travers le temps. La performance de la méthode skywis plot pour la capture du signal démographique contenu dans les séquences contemporaines d'ADN, a été illustrée par simulation, en utilisant plusieurs scénarios démographiques pour lesquels la taille de la population e ective varie de manière modérée . Il s'est avéré que le skywis plot permet de reconstruire correctement l'historique démographique récent des séquences selon plusieurs scénarios démographiques proposés. En particulier, notre méthode permet de capter les points de changement de la taille de la population e ective. De plus, on a trouvé que la performance du skywis plot est comparable à la méthode skyline plot bayésien qui utilise des techniques phylogénétiques et un échantillonnage MCMC. La méthode a été ensuite généralisée au cas d'un échantillonnage hétérochrone, où, en plus d'introduire le cadre méthodologique adéquat en adaptant la fonction d'importance de Stephens et Donnelly (2000), il a été illustré par simulation qu'il est possible, en présence de telles séquences hétérochrones, d'améliorer la performance du skywis plot dans le cas d'une croissance exponentielle de la taille de la population e ective. Cela est encore plus marquant à l'approche du temps de l'ancêtre commun, puisque cela permet l'ajout d'information qui est béné que à la méthode au moment de la reconstruction des généalogies qui se fait, rappelons-le, du présent vers le passé. La méthode skywis plot permet de bien reconstruire l'historique démographique dans des cas où le changement de la taille de la population n'est pas brutal. Par contre, cette approche très exible n'arrive pas à bien capter une forte augmentation/réduction de la taille d'une population. Cela nous a amené à développer une seconde méthode, qui est étudiée dans la suite de la thèse. Nous avons donc proposé d'améliorer la performance de la méthode skywis plot, en supposant d'abord la disponibilité d'information supplémentaire sur l'estimé de la taille de la population relative à di érents instants. Techniquement, cela rend le processus du nombre d'événements (coalescence ou mutation) non-homogène et a une incidence majeure sur la méthodologie utilisée pour la simulation des généalogies. Plus particulièrement, la simulation du temps du prochain événement, ainsi que la fonction d'importance utilisée, sont très a ectées. Cette nouvelle méthode a été appelée, calibrated skywis plot, car l'estimation de la taille de la population relative aux temps d'échantillonnage nous permet de simuler di éremment les temps entre deux événements en opérant un calibrage sur chaque intervalle inter-échantillonal. L'hypothèse de l'existence d'une estimation au préalable de la taille de la population relative à di érents moments a été ensuite levée, en proposant une procédure itérative, iterative calibrated skywis plot. Dans cette méthode, la taille de la population e ective est ainsi approximée par une fonction en escalier, où les estimés sont réestimés après chaque itération en utilisant la méthode calibrated skywis plot. Ces fonctions en escalier sont utilisées pour générer les temps d'attente d'un processus de Poisson non homogène (coalescence avec mutation) sous un modèle avec une taille de population variable. Cela nous a amené à adapter la distribution proposée de Stephens et Donnelly (2000). Comme illustration, nous avons appliqué la méthode iterative calibrated skywis plot sur un ensemble de données simulées à partir d'un modèle où la taille de la population e ective évolue de manière exponentielle, à croissance rapide. Nous avons montré que la nouvelle méthode améliore nettement le résultat trouvé par la méthode skywis plot. Dans le futur, nous prévoyons généraliser notre ensemble de méthodes skywis plot en incluant la recombinaison, qui induit une structure de graphe, plutôt que d'arbre. En e et, contrairement aux méthodes basées sur la phylogénétique, cela est possible, puisque les méthodes IS ont été déjà développées dans ce contexte (par exemple, Fearnhead and Donnelly, 2001). De plus, nos méthodes pourraient être appliquées à des modèles de substitution plus complexes, ce qui est plus réaliste, notamment dans le cas de virus ARN qui évoluent rapidement. En n, notons que la méthode skywis plot a fait l'objet d'un article publié dans la revue Frontiers in Genetics (Ait Kaci Azzou et al., 2015), tandis que les méthodes calibrated skywis plot et iterative calibrated skywis plot ont fait l'objet d'un deuxième article soumis.